Definieren analoger Sprachfunktionen
Inhalt
Einführung
In diesem Dokument wird beschrieben, wie analoge Sprachsignale gemessen werden, welche Einheiten verwendet werden und welche Bezugspunkte bei der Messung verwendet werden.
Die Qualität eines Übertragungssystems wird durch den Unterschied zwischen gesprochener Sprache an einem Ende und reproduzierter Stimme am anderen Ende bestimmt. Jeder, der das Telefon nutzt, erlebt sowohl gute als auch schlechte Verbindungen und kann die Qualität einer bestimmten Verbindung wahrscheinlich subjektiv beschreiben. Aber wie kann man gute und schlechte Qualität objektiv definieren?
Bei der Übermittlung besteht der erste Schritt zur Beantwortung dieser Frage darin, über folgende Fragen zu entscheiden:
-
Was ist zu messen?
-
Was sind die Maßeinheiten?
-
Was ist der Bezugspunkt für die Messungen?
Dieses Dokument beantwortet diese Fragen.
Voraussetzungen
Anforderungen
Für dieses Dokument bestehen keine speziellen Anforderungen.
Verwendete Komponenten
Dieses Dokument ist nicht auf bestimmte Software- und Hardwareversionen beschränkt.
Konventionen
Weitere Informationen zu Dokumentkonventionen finden Sie in den Cisco Technical Tips Conventions (Technische Tipps zu Konventionen von Cisco).
Analoge Sprachmerkmale
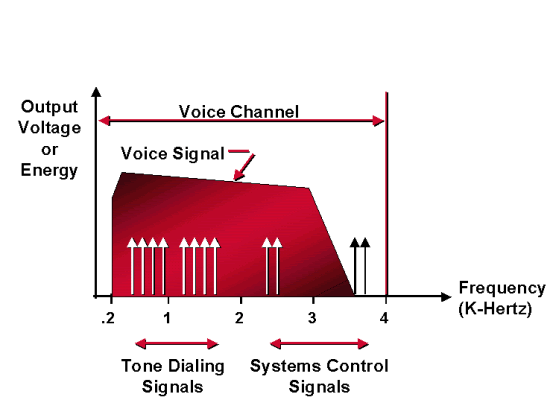
Analog ist definiert als ein Signal mit einer kontinuierlich und gleichmäßig variierenden Amplitude oder Frequenz. Menschliche Sprache und alles andere, was man hört, ist analog, und auch frühe Telefonsysteme waren analog. Analoge Signale werden oft als glatte Sinuswellen dargestellt, aber Sprache und andere Signale sind komplexer als das, da sie viele Frequenzen enthalten. Die Abbildung im Abschnitt Analog Voice Measurement zeigt die typische Energieverteilung in Sprachsignalen.
Die vertikale Achse ist relative Energie und die horizontale Achse ist Frequenz. Die Abbildung im Abschnitt Analog Voice Measurement zeigt, dass die Sprachfrequenzen, die zur Sprache beitragen, von unter 100 Hertz bis über 6000 reichen können. Der Großteil der Energie, die für verständliche Sprache erforderlich ist, ist jedoch in einem Frequenzband zwischen 200 und 4000 enthalten.
Um unerwünschte Signale (Geräusche) zu vermeiden, die Gespräche stören oder Fehler in Steuersignalen verursachen können, sind die Leitungen, die die Telefonsignale übertragen, so ausgelegt, dass sie nur bestimmte Frequenzen übertragen. Die Frequenzbereiche, die überschritten werden, sollen im Pass-Band liegen. 0 bis 4000 Hertz ist das Passband eines Telefonsystem-Sprachkanals - ein VF-Kanal. (Manchmal wird diese Band als Meldungskanal bezeichnet.) Die Bandbreite ist der Unterschied zwischen der oberen und der unteren Grenze des Pass-Bands. Daher beträgt die Bandbreite des VF-Kanals 4000 Hertz. Die Sprachübertragung erfordert jedoch nicht den gesamten VF-Kanal. Das Voice-Pass-Band ist auf 300 bis 3300 Hertz beschränkt. Daher wird jedes Signal auf dem Telefonkreislauf, das im Bereich von 300 bis 3300 Hertz liegt, als In-Band-Signal bezeichnet. Jedes Signal, das sich nicht innerhalb der 300 bis 3300 Hertz-Bänder befindet, aber innerhalb des VF-Kanals liegt, wird als Out-of-Band-Signal bezeichnet. Alle Sprachsignale sind In-Band-Signale. Einige Signalisierübertragungen sind In-Band-Übertragungen, andere Out-of-Band-Übertragungen.
Messung analoger Sprachfunktionen
Jede Wellenform kann in Bezug auf Frequenzen und Leistung charakterisiert werden. Die Mengen, die üblicherweise zur Beschreibung verschiedener Aspekte der Übertragungsleistung verwendet werden, sind Frequenz und Leistung. Viele Leistungsstandards werden in Bezug auf die Leistung in einer bestimmten Frequenz angegeben. Die Maßeinheit für die Frequenz ist der Hertz, abgekürzt als Hz oder sichtbar mit dem f-Symbol. Hertz ist ein Zyklus (0,0000000125) oder eine Schwingung pro Sekunde und misst die Wellen oder Frequenzen elektrischer Veränderungen pro Sekunde.
Wie in den meisten elektrischen Systemen wird die Leistung in Watt-Einheiten, abgekürzt W, gemessen. Da die Leistung in Übertragungssystemen relativ gering ist (im Vergleich zur Leistung einer Glühbirne), wird die Leistung in der Regel in Milliwatt ausgedrückt, abgekürzt mW.
1 mW = 1 W = 0.001W = 10–3W
————
1000
Bei der Übertragung ist das gemeinsame Interesse eher an den Machtverhältnissen als an der absoluten Macht. Darüber hinaus ist die Übertragung mit einem sehr großen Bereich von absoluten Leistungswerten verbunden. Aus diesen Gründen wird in der Regel ein praktischer mathematischer Ausdruck relativer Macht, die Dezibel (dB), verwendet. Um die relative Leistung in Form von Dezibel zu beschreiben, müssen Sie den Bezugspunkt definieren, an dem Sie messen. Basierend auf dem gemessenen Übertragungsparameter können Sie verschiedene Formen der Dezibel-Messung verwenden. Jede Messform verfügt über einen speziellen Referenzpunkt. Wenn Sie die entsprechenden Leistungseinheiten für spezifische Referenzen verwenden, können Sie absolute Leistung, relative Leistung und Leistungsgewinne und -verluste messen.
Milliwatt und Hertz
Da die Leistung in Telefonschaltungen klein ist, wird der Milliwatt als Grundleistungsmessgerät verwendet, ebenso wie der Fuß als einfache Längenmessung verwendet wird. Die meisten Messungen der absoluten Leistung bei der Übertragung werden in Milliwatt oder in Einheiten vorgenommen, die direkt mit Milliwatt verwandt sind.
Die Frequenzen, die bei Tests verwendet werden, fallen in der Regel in das Sprachfrequenzband. Üblicherweise verwendete reine (Sinuswellentesttöne) sind 404 Hz, 1004 Hz und 2804 Hz. (Der 4-Hz-Offset wird nicht immer angegeben. Die tatsächlichen Testfrequenzen sollten jedoch um 4 Hz verrechnet werden, um die Auswirkungen auszugleichen, die einige Trägereinrichtungen auf Testtöne haben.) Eine Messung von 1004 Hz liegt in der Nähe der Sprachbandfrequenzen, die einen großen Teil der Sprachleistung übertragen, 404 Hz befindet sich nahe am unteren Ende des Spektrums und 2804 Hz liegt im Bereich der Hochfrequenzkomponenten des Sprachspektrums, die für die Verständlichkeit von Sprache wichtig sind ...
Neben reinen Testtönen wird für bestimmte Tests auch "weißes Rauschen" innerhalb bestimmter Frequenzbereiche verwendet. White Noise Testtöne sind komplexe Wellenformen, deren Leistung gleichmäßig über den Frequenzbereich verteilt ist. "Weißes Geräusch" ist ein Signal, das alle Audiofrequenzen in gleichen Mengen enthält, jedoch keine erkennbaren Tonsignale oder -töne aufweist.
Diese Abbildung veranschaulicht ganz allgemein und vereinfacht, wie eine Testtonübertragung eingerichtet wird und wie Testtöne generiert und gemessen werden (Demarche A bis Demarche B).
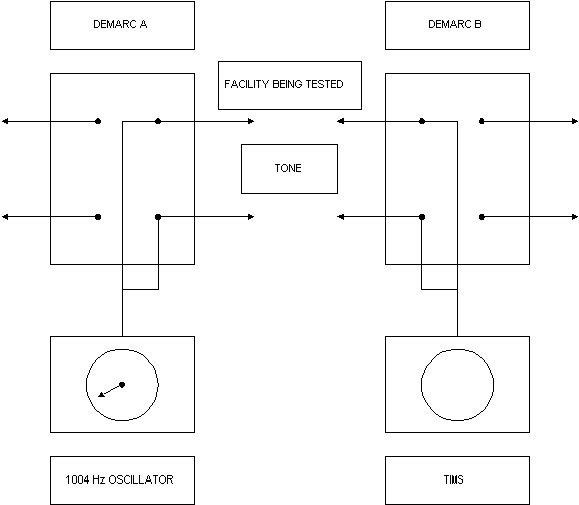
Das Gerät ist so eingerichtet, dass der Stromkreis zwischen der Demarke von A und der Demarke von B geprüft wird. Sie messen den Verlust von 1004 Hz, der im Stromkreis zwischen A und B auftritt.
Die Bridging-Clips an beiden Demarchen werden entfernt, um das zu prüfende Segment des Stromkreises zu isolieren.
Bei A wird ein Oszillator angeschlossen, um Leads zu übertragen und zu empfangen (auch als Tipp- und Ring-Leads bezeichnet). Bei B wird ein Übertragungsmessgerät (TIMS) zum Senden und Empfangen von Leads angebracht.
Der Oszillator bei A ist so eingestellt, dass ein reiner Testton mit einer Leistung von 1 mW bei 1004 Hz erzeugt wird. Bei Demarke B ist die TIMS auf Leseleistung im Bereich von 1 mW eingestellt. Die Leistungsaufnahme bei B beträgt 0,5 mW. Daher ist die zwischen A und B verlorene Leistung:
1 mW – 0.5 mW = 0.5 mW
Eine nützlichere Möglichkeit, den Verlust auszudrücken, ist der relative Verlust oder das Verhältnis zwischen Stromausgang (B) und Leistung in (A):
Relative loss = Power out (B)
——————————————
Power in (A)
Relative loss = 0.5 x 10-3
——————————————
1 X 10-3
Relative loss = 0.5
Half the power that the 1004 Hz test-tone introduced at A is lost by the time
it reaches B.
In diesem Beispiel wird der Test wiederholt, wenn weniger Testton-Power verwendet wird. Der Oszillator bei Demarke A ist so eingestellt, dass er 1004 Hz Ton bei einer Leistung von 0,1 mW erzeugt. Bei Demarke B beträgt die Leistungsmessung 0,05 mW. Der absolute Leistungsverlust ist dann:
0.1 mW – 0.05 mW = 0.05 mW
Der relative Verlust bzw. das Verhältnis zwischen Stromausgang (B) und Leistung in (A) beträgt:
Relative Loss = Power out(B)
——————————————
Power in (A)
Relative Loss = 0.05 x 10-3
—————————————
1 x 10-3
Relative Loss = 0.5
Der relative Verlust bzw. das Leistungsverhältnis zwischen B und A ist gleich, ob ein Testsignal von 1 mW oder 0,1 mw verwendet wird.
Der Dezibel
Mathematisch ist die Dezibel eine logarithmische Maßeinheit. Der Logarithmus (Logarithmus) einer bestimmten Zahl ist die mathematische Leistung, auf die eine Basisnummer erhöht werden muss, um zu einer bestimmten Zahl zu führen. Die Basisnummer, die Sie für die Dezibel verwenden, lautet 10. Was ist beispielsweise der Logarithmus (log) von 100? Eine andere Möglichkeit, diese Frage zu stellen, ist "Zu welcher Macht heben Sie 10, um 100 zu bekommen?". Die Antwort ist 2, weil 10 x 10 = 100.
In ähnlicher Weise
log (100)= 2
log (1000)= 3
log (10,000)= 4
usw.
Sie können auch Logarithmen verwenden, um Bruchmengen auszudrücken. Was ist zum Beispiel der Logarithmus von 0,001? Eine andere Möglichkeit, diese Frage zu stellen, ist "Zu welcher Macht heben Sie 1/10 (0,1), um 0,001?". Die Antwort lautet 3. Das Protokoll einer Bruchzahl wird standardmäßig als negativ ausgedrückt.
log (0.001) = -3
Logarithmen von Zahlen, die keine ganzzahligen Kräfte von 10 sind, können berechnet werden, wenn Sie sie in einer Tabelle nachschlagen oder wenn Sie einen Handrechner verwenden.
Die Dezibel verwendet Logarithmen, um die Leistungswerte auszudrücken. Der DeciBel, dB, ist definitionsgemäß das logarithmische (Basis 10) Quotient zweier Kräfte, P1 und P2, das durch folgende Werte angegeben wird:
dB = 10 log P2
——
P1
P2 und P1 sind Leistungsmessungen, die in konsistenten Einheiten ausgedrückt werden. Die Anzahl der Dezibel ist positiv, wenn P2 größer als P1 ist. Die Zahl ist negativ, wenn P1 größer als P2 ist (siehe Tabelle). Es ist wichtig, dass die beiden Kräfte in den gleichen Einheiten ausgedrückt werden, wie milliWatt (mW) oder Watt (W). Andernfalls führt dies zu Berechnungsfehlern.
| Leistungsverhältnis | dB-Wert |
|---|---|
| 2 | 3* |
| 4 | 6* |
| 8 | 9* |
| 10 | 10 |
| 100 | 20 |
| 1000 | 30 |
| 100.000 | 50 |
| 100000000 | 90 |
* Ungefährer dB-Wert.
Das Leistungsverhältnis zwischen der bei B gemessenen Leistung und der bei A gemessenen Leistung betrug eine Hälfte. In Dezibel ausgedrückt:
(Loss, A to B) = 10 log (0.5) (Loss, A to B) = –3 dB
Mit Dezibel können Sie den Verlust oder Gewinn eines Stromkreises oder eines Gerätes ausdrücken, ohne die tatsächlichen Werte der Ein- und Ausgangsleistung explizit angeben zu müssen. Im Beispiel beträgt der Verlust zwischen A und B immer 3 dB, unabhängig von der absoluten Menge der übertragenen Energie.
Entscheidende Messung im Verhältnis zu einem Milliwatt
Absolute Leistung wird in Milliwatt ausgedrückt, relative Leistung in Dezibel. Wenn Sie eine Beziehung zwischen dem Dezibel und dem Milliwatt herstellen, können Sie das Milliwatt als operative Maßeinheit eliminieren und ausschließlich mit der Dezibel- und damit verbundenen Maßeinheit umgehen. Die Maßeinheit, die verwendet wird, um absolute Macht in Form von Dezibel auszudrücken, ist dBm.
dBm = 10 log (Power, measured in mW)
—————————————————————————
1 mW
Da ein Milliwatt der Standardleistungsreferenz in der Kommunikation ist, ist es logisch, dass 0 dBm (der absolute Leistungsreferenzwert bei Verwendung von Dezibeleinheiten) 1 mW Leistung entspricht. Mathematisch:
0 dBm = 10 log Power out
——————————
Power in
0 dBm = 10 log (1/1)
0 dBm = 10 x 0 = 0
Da die Leistung eine Wechselstromwellenform ist und die Impedanz je nach Frequenz variieren kann, muss angegeben werden, auf welcher Frequenz der 0 dBm-Standard basiert. Die Standardfrequenz beträgt 1004 Hz.
Sie müssen auch den Widerstand oder Impedanz (Belastung) des Schaltkreises kennen. Die Standard-Impedanz ist 600 Ohm.
Daher entspricht die Referenz von 0 dBm 1 mW an Leistung, die bei einem Impedanz von 600 Ohm mit einer Frequenz von 1004 Hz eingestellt wird.
Die Tests werden in der Regel mit Testsignalen durchgeführt, die weniger als 1 mW (0 dBm) leistungsfähig sind. Wenn Sie einen 1004-Hz-Testton von -13 dBm bei A anwenden, lesen Sie -16 dBm bei der TIMS bei B. Der Verlust beträgt weiterhin -3 dB.
Übertragungspunkt
Bei jeder Diskussion über die Leistung eines Stromkreises ist es erforderlich, die Leistung an einem bestimmten Punkt in einem Stromkreis unter Bezugnahme auf die Leistung zu beschreiben, die an anderen Stellen im Stromkreis vorhanden ist. Diese Leistung kann Signal-Leistung, Rauschen oder Testtöne sein.
Die Beschreibung dieser Kraft ähnelt der Beschreibung der Höhe eines Berges (oder der Tiefe des Ozeans). Um die Höhe eines Berges zu messen, ist es notwendig, eine Referenzhöhe zu wählen, von der die Messung erfolgt. Die Standardreferenzhöhe ist der Meeresspiegel, dem willkürlich eine Höhe von Null zugewiesen wird. Wenn man alle Berge vom Meeresspiegel abmisst, kann man Vergleiche ihrer Höhe anstellen, auch wenn sie viele Kilometer voneinander entfernt sein können.
Diese Abbildung zeigt die Tonübertragung von Demarke A zu Demarkt B.

Ähnlich kann die Leistung an bestimmten Stellen in einem Stromkreis in Bezug auf die Leistung an einem standardmäßigen Bezugspunkt beschrieben werden.
Dieser Punkt, der dem Meeresspiegel entspricht, wird als Nullübertragungspunkt oder 0 TLP bezeichnet.
Jeder andere TLP kann auf die 0 TLP verwiesen werden, indem algebraisch die Gewinne und Verluste von 1004 Hz vom 0 TLP bis zum Messpunkt summiert werden.
Die an einem bestimmten Punkt in einem Stromkreis vorhandene Leistung hängt von der Leistung an der Signalquelle, von dem Ort, an dem die Quelle angewendet wird, und vom Verlust oder Gewinn zwischen den beiden jeweiligen Punkten ab.
Bei Verwendung des 0-TLP-Konzepts wird die Leistung in einem Stromkreis beschrieben, indem angegeben wird, wie hoch die Leistung wäre, wenn sie bei der 0-TLP genau gemessen würde. Die Standardnotation lautet dBm0, d. h. die auf die 0-TLP referenzierte Leistung.
Beispiel: Der Begriff -13 dBm0 bedeutet, dass die Leistung bei 0 TLP -13 dBm beträgt. Ein richtig eingerichtetes TIMS misst -13 dBm an der 0-TLP. Ein Beispiel für ein -13 dBm0-Signal.
Sobald die Leistung an der 0-TLP gefunden wurde, kann die Leistung an einem anderen Punkt des Stromkreises problemlos bestimmt werden. Wenn das Signal beispielsweise bei 0 TLP -13 dBm beträgt, ist l3 dB niedriger als der numerische Wert einer beliebigen TLP auf dem Stromkreis, gemessen an dieser TLP.
Wenn das Signal bei 0 TLP -13 dBm (macht es zu einem -13-dBm0-Signal) beträgt, kann die Leistung bei +5 TLP berechnet werden, wie die folgende Ausgabe zeigt:
(TLP) + (Power at the 0 TLP) = Power at the +5 TLP) (+5)+(–13 dBm0) = –8 dBm
Wenn das -13-dBm0-Signal bei +5 TLP richtig gemessen wird, lautet der Messwert -8 dBm.
Wenn ein -13-dBm0-Signal an der TLP -3 gemessen wird, lautet der Messwert -16 dBm auf ähnliche Weise:
(TLP) + (Power at the 0 TLP) = (Power at the –3 TLP) (–3)+(–13 dBm0) = –16 dBm
Um die erwartete Leistung an einer beliebigen TLP zu bestimmen, reicht es aus, die Leistung einer anderen TLP im Schaltkreis zu kennen. Und genau wie der Berg nicht in der Nähe des Meeres sein muss, um seine Höhe zu bestimmen, muss die 0 TLP nicht tatsächlich auf der Strecke existieren.
Diese Abbildung veranschaulicht einen Stromkreis zwischen zwei Demarks. Beim -16 TLP wird ein -29-dBm-Testtonsignal angewendet. Was sollten Sie bei der +7 TLP messen?
Auch wenn die 0-TLP nicht in der Schaltung vorhanden ist, können Sie die Leistung beschreiben, die Sie bei der 0-TLP sehen, wenn sie vorhanden ist:
TLP)+(Power at 0 TLP) = (Power at the –16 TLP)
(–16)+(Power at 0 TLP) = –29 dBm
(Power at 0 TLP) = –13 dBm
Wenn Sie die Beziehung erneut verwenden, können Sie die Leistung an der + 7 TLP ermitteln:
(TLP)+ (Power at 0 TLP) = (Power at + 7 TLP) (+7)+(–13 dBm0) = –6 dBm
Die Verwendung der 0-TLP-Referenz ermöglicht die Angabe von Übertragungszielen und Messergebnissen unabhängig von einer bestimmten TLP und ohne Angabe der zu verwendenden Testtonwerte oder des zu verwendenden Testtons.
Diese Abbildung zeigt eine Tonübertragung von Demarke A zu Demarkt B.

Geräuschmesseinheiten
Zusätzlich zur Beschreibung der Ton-Leistung an verschiedenen Stellen in einem Stromkreis können dezibel-bezogene Maßeinheiten verwendet werden, um das Geräusch in einem Stromkreis zu beschreiben.
Brn
Um die Leistung in einem Stromkreis zu beschreiben, wird der Begriff dBm verwendet, was "Leistung, die auf 1 mW verweist". Da Rauschen in der Regel viel weniger als 1 mW an Leistung enthält, empfiehlt es sich, eine Referenzleistung zu verwenden, die viel kleiner als 1 mW ist. Die in der Beschreibung des Rauschens verwendete Bezugsleistung beträgt -90 dBm. Die Notation, die für die Beschreibung von Rauschen als Referenzgeräusch verwendet wird, lautet "dBrn". Wenn Sie den Rauschpegel in dBm kennen, können Sie das Geräusch in dBrn leicht messen:
dBrn = dBm + 90 dB
Eine Geräuschmessung von 30 dBrn gibt beispielsweise einen Leistungsgrad von -60 dBm an (30 dB über dem Referenzrauschpegel von -90 dBm). Diese Tabelle zeigt die Beziehung zwischen dBm0 und dBrn.
| dBm0 | dB-Wert |
|---|---|
| 0 | 90 |
| 10 | 80 |
| 20 | 70 |
| 30 | 60 |
| 40 % | 50 |
| 50 % | 40 |
| 60 % | 30 |
| 70 % | 20 |
| 80 % | 10 |
| 90 % | 0 |
DBrnC
Das Geräusch enthält zahlreiche unregelmäßige Wellenformen, die eine große Bandbreite an Frequenzen und Kräften aufweisen. Obwohl jedes Geräusch, das über ein Gespräch hinausgeht, störend wirkt, haben Versuche gezeigt, dass die Störungswirkung am größten ist in der Mitte des Frequenzbands.
Um eine nützliche Messgröße für die Störungswirkung von Lärm zu erhalten, werden die verschiedenen Frequenzen, die zum Gesamtlärm beitragen, auf der Grundlage ihrer relativen Störwirkung gewichtet. Diese Gewichtung erfolgt durch die Verwendung von Gewichtungsnetzwerken oder Filtern innerhalb von TIMS.
Geräuschmessungen über ein C-Message-Gewichtungsnetzwerk werden in Einheiten von dBrnC ausgedrückt (Rauschen über Referenzgeräusch, C-Message-Gewichtung).
DBrnCO
Wie bei der Ton-Leistung kann auf die Rauschleistung der TLP 0 verwiesen werden.
Wenn beispielsweise das Rauschziel für den Stromkreis 31 dBrnC0 ist, wie lautet die Geräuschmessung bei der +7 TLP?
TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(+7) + (31 dBrnC0) = 38 dBrnC
Die Rauschmessung an der +7-TLP beträgt 38 dBrnC.
Was ist die Geräuschmessung bei der TLP -16?
(TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(–16) + (31 dBrnC0) = 15 dBrnC
Die Rauschmessung an der TLP -16 beträgt 15 dBrnC.
 Feedback
Feedback